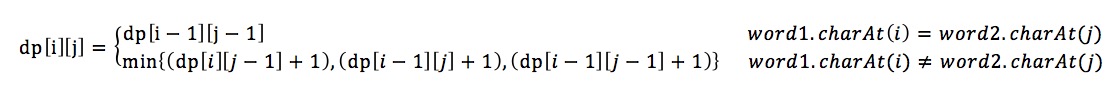Leetcode 72 Edit Distance
The problem description is as follow:
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.) You have the following 3 operations permitted on a word: a) Insert a character b) Delete a character c) Replace a character
This is a classical DP problem. I use a 2-D matrix dp[][] to save all the data. dp[i][j] stands for the edit distance between two strings with length i and j, word1[0,...,i-1] and word2[0,...,j-1].
Now we only have to figure how to get the recursive formula for dp[i][j] from historical data we already got, which is equivalent to getting the relationship between dp[i][j] and dp[i-1][j-1] . Let’s say we transform from string word1 to string word2. The first string has length i and it’s last character is word1.charAt(i) = x; the second string has length j and its last character is word2.charAt(j) = y.
1. if x == y, then dp[i][j] == dp[i-1][j-1] 2. if x != y, and we insert y for word1, then dp[i][j] = dp[i][j-1] + 1 3. if x != y, and we delete x for word1, then dp[i][j] = dp[i-1][j] + 1 4. if x != y, and we replace x with y for word1, then dp[i][j] = dp[i-1][j-1] + 1 When x!=y, dp[i][j] is the min of the three situations.
And we have the initial condition as dp[i][0] = i, dp[0][j] = j
Here comes the code:
public class Solution {
public int minDistance(String word1, String word2) {
int L1 = word1.length();
int L2 = word2.length();
// L1+1, L2+1, because finally return dp[L1][L2]
int[][] dp = new int[L1 + 1][L2 + 1];
for (int i = 0; i <= L1; i++) {
dp[i][0] = i;
}
for (int j = 0; j <= L2; j++) {
dp[0][j] = j;
}
//iterate though, and check last char
for (int i = 0; i < L1; i++) {
char c1 = word1.charAt(i);
for (int j = 0; j < L2; j++) {
char c2 = word2.charAt(j);
//if last two chars equal
if (c1 == c2) {
//update dp value for +1 length
dp[i + 1][j + 1] = dp[i][j];
} else {
int replace = dp[i][j] + 1;
int insert = dp[i][j + 1] + 1;
int delete = dp[i + 1][j] + 1;
int min = replace > insert ? insert : replace;
min = delete > min ? min : delete;
dp[i + 1][j + 1] = min;
}
}
}
return dp[L1][L2];
}
}