How to tell if two linked lists intersect V.S. How to detect linked list cycle

How to tell if two linked lists intersect V.S. How to detect linked list cycle

I am really excited to bring this, it’s gonna be fun, hope you enjoy.

Edit Leetcode 141: Linked List Cycle on GitHub

Let’s start with a few problems in leetcode 141: Linked List Cycle

Given a single linked list, determine if it has a cycle in it.
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */

If a single linked list has cycle, how are we supposed to know that? Pretty straight-forward:

1. Define 2 nodes that points to the header of linked list.
2. Node 1 traverses faster than Node 2, say twice the speed.
3. If the linked list contains a cycle, then Node 1 and Node 2 will meet at some time.

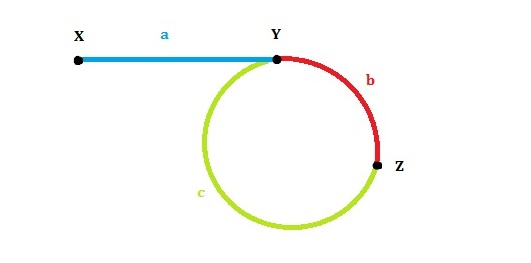
Here’s a picture for illustration:

In the picture above, the header of linked list is X. Node 1 and Node 2 follow the direction of X->Y->Z. It is obvious that they will meet as long as their speed is different. Here comes the easiest part:

 public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while(fast!=null&&fast.next!=null){
            fast=fast.next.next;
            slow=slow.next;
            if(fast==slow){
                return true;
            }
        }
        return false;
    }
}

Edit Leetcode 142: Linked List Cycle II on GitHub

Now let’s spice up a little. Check leetcode 142: Linked List Cycle II.

How to find where the cycle begins, that is to say, how to find the first node (Node Y in the picture above) of the cycle?

This is just a extension of the problem above. We are still going to define a fast node and slow node:

ListNode fast = head;
ListNode slow = head;
fast = fast.next.next;
slow = slow.next;

Since the speed of fast node is twice of slow node, the distance should also be twice if they share the same time. Assume both nodes start at X at the same time and meet at node Z. From our previous observation, there should be:

a+b+c+b = 2*(a+b)
a = c

Now we just have to assign a new node at X with the speed of slow node. If the new node starts at X and slow node starts at Z at the same time, they are guaranteed to meet at Y, which is the first node of the cycle. Here comes the easiest part:

 public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast=head;
        ListNode slow=head;
        while(fast!=null&&fast.next!=null){
            fast=fast.next.next;
            slow=slow.next;
            
            if(fast==slow){
                ListNode a1 = head;
                while(slow!=a1){
                    slow=slow.next;
                    a1=a1.next;
                }
                return a1;
                
            }
        }
        return null;
    }
}

Now let’s extend the previous question:

How to detect if two linked lists intersect?

1. First, if both singly linked lists contains no cycle (please don’t ask me how to detect if linked list contains cycle):

Since both are singly linked lists, if they intersects, the intersection must be the end of both linked list.

1) Traverse the first linked list, get tail node a
2) Traverse the second linked list, get tail node b
3) If a==b, then two linked lists intersects;
   If not, then they don't intersects.

2. If one contains cycle and the second doesn’t, they can’t intersect.

3. If both contains cycle, we need further discussion. Let’s assume the first linked list as following again:

We can simply get node Y, as well as any node on the cycle. We just have to check if node Y or any other node on the first linked list is on the second linked list.

1) Traverse the first linked list and get Node Y (first node in cycle)
2) Traverse second linked list to see if node Y is in second linked list
3) If node Y from first linked list is in the second linked list, then two list intersects.
   If not, they don't intersects.

How to get the first node of intersection of two linked lists?

1. If both linked lists contain no cycle and intersects:

1) Get length of first linked list A, assume A.length = l1
2) Get length of second linked list B, assume B.length = l2 and l2>l1
3) Traverse list B (l2-l1) steps first.
4) Start traversing list A and continue traversing list B at the same time.
5) They will meet at the first node of intersection.

2. If both linked lists contain cycle and intersects, assume first linked list A as follow:

1) Define the length of a linked list that contains cycle as: A.length = a+b+c 
2) Get length of first linked list A, assume A.length = l1
3) Get length of second linked list B, assume B.length = l2 and l2>l1
4) Traverse list B (l2-l1) steps first.
5) Start traversing list A and continue traversing list B at the same time with the same speed.
6) They will meet at the first node of intersection.