Leetcode 145 Binary Tree Postorder Traversal
The problem description is as follow:
Given a binary tree, return the postorder traversal of its nodes' values.
For example:
Given binary tree {1,#,2,3},
1
\
2
/
3
return [3,2,1].
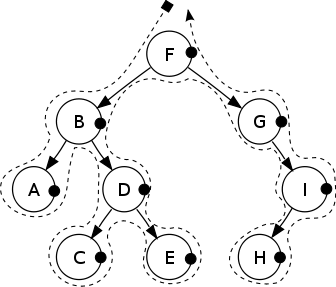
In case you are not familiar with postorder tree traversal, the following graph would help:
The postorder traversal for previous tree is A, C, E, D, B, H, I, G, F.
Recursive Approach
![]() Edit Binary Tree Postorder Traversal on GitHub
Edit Binary Tree Postorder Traversal on GitHub
Recursive approach is pretty straight forward. The order of postorder is :
1. Left Child 2. Right Child 3. Parent Node
Thus the code will be:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result=new ArrayList<Integer> ();
if (root==null){
return result;
}
builder(root, result);
return result;
}
private void builder(TreeNode root, List<Integer> result){
if (root==null){
return;
}
builder(root.left, result);
builder(root.right, result);
result.add(root.val);
}
}
The time complexity of recursive approach is O(n) since we are just traversing the whole tree once. The space complexity of recursive approach is O(log n).
Iterative Approach
![]() Edit Binary Tree Postorder Traversal on GitHub
Edit Binary Tree Postorder Traversal on GitHub
When it comes to iterative approach in tree traversal, always use a stack or queue. We could use a stack to imitate the recursive process we did above:
public class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if(root == null) {
return res;
}
LinkedList<TreeNode> stack = new LinkedList<TreeNode>();
TreeNode pre = null;
TreeNode p =root;
while(p != null || !stack.isEmpty()) {
if(p!=null) {
stack.push(p);
p = p.left;
}
else {
TreeNode peekNode = stack.peek();
if(peekNode.right!=null && pre != peekNode.right) {
p = peekNode.right;
}
else {
stack.pop();
res.add(peekNode.val);
pre = peekNode;
}
}
}
return res;
}
}
The time complexity of recursive approach is O(n) since we are just traversing the whole tree once. The space complexity of recursive approach is O(log n).
Morris Traversal Algorithm
![]() Edit Binary Tree Postorder Traversal on GitHub
Edit Binary Tree Postorder Traversal on GitHub
Actually there’s a better way to solve the problem. Instead of using O(log n) space, we could solve it with O(l) space.
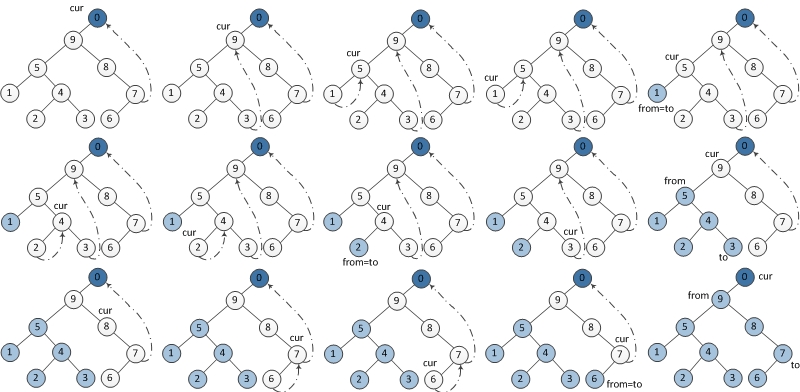
In order to solve the problem with O(l) space, the most important question is how to traverse back to parent node from child node. Morris traversal introduce threaded binary tree. In threaded binary tree, we don’t have to assign additional space to every node pointing to the predecessor and successor, nor do we have to save the nodes into stack.
Set current node as temporary node, name dump 1. If left child of current node is empty, set current node = current node's right child 2. If left child of current node is not empty, find the in-order traversal predecessor node in its left subtree - If predecessor's right child is empty, set predecessor's right child = current node. Set current node = current node's left child. - If predecessor's right child is current node, set predecessor's right child back to empty (recover structure of tree). Reversely output nodes from current node's left child to current node's predecessor (in other words, from current node's predecessor to current node's left child). Set current node = current node's right child. - There won't be other possibility according to definition of predecessor. Repeat process 1 and 2 until current node is empty.
The following graph would help a lot:
Here comes the code:
public class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
TreeNode dummy = new TreeNode(-1);
dummy.left = root;
TreeNode cur = dummy;
TreeNode pre = null;
while(cur!=null) {
if (cur.left==null) {
cur = cur.right;
}
else {
pre = cur.left;
while (pre.right!=null && pre.right!=cur)
pre = pre.right;
if (pre.right==null) {
pre.right = cur;
cur = cur.left;
}
//Reversely output nodes from current node's left child
//to current node's predecessor
else {
reverse(cur.left, pre);
TreeNode temp = pre;
while (temp != cur.left) {
res.add(temp.val);
temp = temp.right;
}
res.add(temp.val);
reverse(pre, cur.left);
pre.right = null;
cur = cur.right;
}
}
}
return res;
}
private void reverse(TreeNode start, TreeNode end) {
if (start == end)
return;
TreeNode pre = start;
TreeNode cur = start.right;
TreeNode next;
while (pre != end) {
next = cur.right;
cur.right = pre;
pre = cur;
cur = next;
}
}
}
Since we are traversing each node at most 3 times, the time complexity is still O(n) and we are only using O(1) extra space.