Leetcode 208 Implement Trie (Prefix Tree)

Introduction to Prefix Tree

In case anyone is not familiar with Trie (Prefix Tree), I will just do a quick explanation. Let’s see what wiki says:

In computer science, a trie, also called digital tree and sometimes radix tree or prefix tree (as they can be searched by prefixes), is an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings.

Alright, this means nothing without further illustration. The following graphs of prefix tree will help a lot.

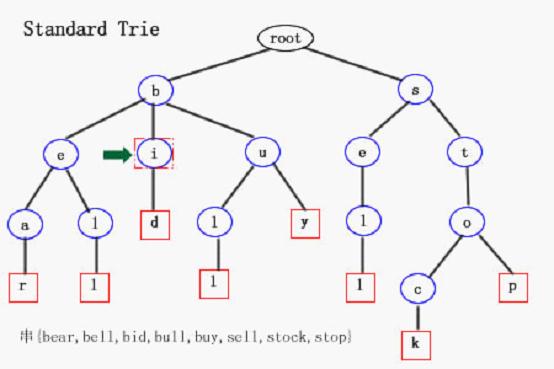
Example 1:

Set of Strings: {bear, bell, bid, bull, buy, sell, stock, stop}

Prefix Tree for Set of Strings:

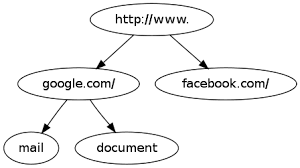
Example 2:

Set : {http://www.google.com/mail, http://www.google.com/document, http://www.facebook.com}

Prefix Tree for Set:

How to Find a String in Standard Trie

For simplicity, I will only take the standard trie with English letters into consideration.

We could have each node in the standard trie to contain a children array which length is 26 (the number of English letters). If we want to get the character ‘a’, we get the 1st element of children array. If we want to get the character ‘z’, we get the 26th element of children array.

Take the first graph above and the word “bull” as example:

1. Check the ('b'-'a'=)1st element in the children array of root node, if the node is not empty, locate to the node. In this case, the 1st element in the children array of root node is node b.
2. Check the ('u'-'a'=)20th element in the children array of node b, if the node is not empty, locate to the node. In this case, the 20th element in the children array of node b is node u.
3. ... Locate to node l.
4. ... Locate to node l.

Note: If any of the node is empty in the search process, it means the word is not in our set.

Leetcode 208 Implement Trie (Prefix Tree)

Edit Implement Trie (Prefix Tree) on GitHub

Now we are ready to fix this problem, let’s see the problem description first:

Implement a trie with insert, search, and startsWith methods.

Note:
You may assume that all inputs are consist of lowercase letters a-z.

Well, actually I have already give the solution in previous illustration. Since there’s only letters a-z, we could have the TrieNode class as follow:

class TrieNode{
    public TrieNode[] children = new TrieNode[26];
    public String item = "";
}

The Trie class will be:

public class Trie{
    private TrieNode root;
 
    public Trie() {
        root = new TrieNode();
    }
 
    public void insert(String word){
        TrieNode node = root;
        for(char c: word.toCharArray()){
            if(node.children[c-'a']==null){
                node.children[c-'a']= new TrieNode();
            }
            node = node.children[c-'a'];
        }
        node.item = word;
    }
 
    public boolean search(String word){
        TrieNode node = root;
        for(char c: word.toCharArray()){
            if(node.children[c-'a']==null)
                return false;
            node = node.children[c-'a'];
        }
        if(node.item.equals(word)){
            return true;
        }else{
            return false;
        }
    }
 
    public boolean startsWith(String prefix){
        TrieNode node = root;
        for(char c: prefix.toCharArray()){
            if(node.children[c-'a']==null)
                return false;
            node = node.children[c-'a'];
        }
        return true;
    }
}

Note: In class TrieNode , item is to determine whether the node is a leaf node.

Another Approach

Edit Implement Trie (Prefix Tree) on GitHub

Instead of using a children array of  Trie nodes for searching Strings, we could use a HashMap<Character, TrieNode> for searching Strings. In this case, we have to use HashMap.containsKey() and HashMap.get() to drill down the correct path of Trie.

The time efficiency will no longer be O(1) but we could save space by dynamically assigning the size of children node, instead of having a static size of 26.

class TrieNode {
    char c;
    HashMap<Character, TrieNode> children = new HashMap<Character, TrieNode>();
    boolean isLeaf;
 
    public TrieNode() {}
 
    public TrieNode(char c){
        this.c = c;
    }
}
public class Trie2 {
    private TrieNode root;
 
    public Trie() {
        root = new TrieNode();
    }
 
    // Inserts a word into the trie.
    public void insert(String word) {
        HashMap<Character, TrieNode> children = root.children;
 
        for(int i=0; i<word.length(); i++){
            char c = word.charAt(i);
 
            TrieNode t;
            if(children.containsKey(c)){
                    t = children.get(c);
            }else{
                t = new TrieNode(c);
                children.put(c, t);
            }
 
            children = t.children;
 
            //set leaf node
            if(i==word.length()-1)
                t.isLeaf = true;    
        }
    }
 
    // Returns if the word is in the trie.
    public boolean search(String word) {
        TrieNode t = searchNode(word);
 
        if(t != null && t.isLeaf) 
            return true;
        else
            return false;
    }
 
    // Returns if there is any word in the trie
    // that starts with the given prefix.
    public boolean startsWith(String prefix) {
        if(searchNode(prefix) == null) 
            return false;
        else
            return true;
    }
 
    public TrieNode searchNode(String str){
        Map<Character, TrieNode> children = root.children; 
        TrieNode t = null;
        for(int i=0; i<str.length(); i++){
            char c = str.charAt(i);
            if(children.containsKey(c)){
                t = children.get(c);
                children = t.children;
            }else{
                return null;
            }
        }
 
        return t;
    }
}

Note: In class TrieNode , isLeaf is a boolean to determine whether the node is a leaf node.

Note2: We have to save the character char c contained by the current node in class TrieNode since we are not using the static children array as previous approach.

Further Thought

What if the set of Strings is {a, ae, aei, aeio, aeiou} ?

Generally speaking, we have a dilemma when one word in the set is the prefix of another: How Do I Know If It Is A Leaf ?

A simple solution is to append a special character, for example '$' to the end of each word. In this case, we will have the new set as {a$, ae$, aei$, aeio$, aeiou$} . Now no word is prefix of another, problem solved!