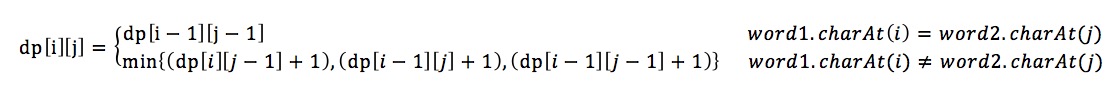Leetcode 72 Edit Distance

Leetcode 72 Edit Distance

Check Edit Distance on GitHub

The problem description is as follow:

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)

You have the following 3 operations permitted on a word:

a) Insert a character
b) Delete a character
c) Replace a character

This is a classical DP problem. I use a 2-D matrix dp[][] to save all the data.  dp[i][j] stands for the edit distance between two strings with length i and j, word1[0,...,i-1] and word2[0,...,j-1].

Now we only have to figure how to get the recursive formula for dp[i][j]  from historical data we already got, which is equivalent to getting the relationship between dp[i][j]  and dp[i-1][j-1] . Let’s say we transform from string word1 to string word2. The first string has length i and it’s last character is word1.charAt(i) = x; the second string has length j and its last character is word2.charAt(j) = y.

1. if x == y, then dp[i][j] == dp[i-1][j-1]
2. if x != y, and we insert y for word1, then dp[i][j] = dp[i][j-1] + 1
3. if x != y, and we delete x for word1, then dp[i][j] = dp[i-1][j] + 1
4. if x != y, and we replace x with y for word1, then dp[i][j] = dp[i-1][j-1] + 1
When x!=y, dp[i][j] is the min of the three situations.

And we have the initial condition as dp[i][0] = i, dp[0][j] = j

Here comes the code:

public class Solution {
    public int minDistance(String word1, String word2) {
        int L1 = word1.length();
        int L2 = word2.length();
     
        // L1+1, L2+1, because finally return dp[L1][L2]
        int[][] dp = new int[L1 + 1][L2 + 1];
     
        for (int i = 0; i <= L1; i++) {
            dp[i][0] = i;
        }
     
        for (int j = 0; j <= L2; j++) {
            dp[0][j] = j;
        }
     
        //iterate though, and check last char
        for (int i = 0; i < L1; i++) {
            char c1 = word1.charAt(i);
            for (int j = 0; j < L2; j++) {
                char c2 = word2.charAt(j);
     
                //if last two chars equal
                if (c1 == c2) {
                    //update dp value for +1 length
                    dp[i + 1][j + 1] = dp[i][j];
                } else {
                    int replace = dp[i][j] + 1;
                    int insert = dp[i][j + 1] + 1;
                    int delete = dp[i + 1][j] + 1;
     
                    int min = replace > insert ? insert : replace;
                    min = delete > min ? min : delete;
                    dp[i + 1][j + 1] = min;
                }
            }
        }
     
        return dp[L1][L2];
    }
}